[Baekjoon] 9020 골드바흐의 추측

[Silver I] 골드바흐의 추측 - 9020

문제 링크

성능 요약

메모리: 25376 KB, 시간: 476 ms

분류

수학(math), 정수론(number_theory), 소수 판정(primality_test), 에라토스테네스의 체(sieve)

문제 설명

1보다 큰 자연수 중에서 1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.

골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 이러한 수를 골드바흐 수라고 한다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다. 예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다. 10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.

2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다.

출력

각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다. 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.

---

에라토스테네스의 체(sieve)

수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.

• 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
• 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
• 자기 자신을 제외한 2의 배수를 모두 지운다.
• 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
• 자기 자신을 제외한 3의 배수를 모두 지운다.
• 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
• 자기 자신을 제외한 5의 배수를 모두 지운다.
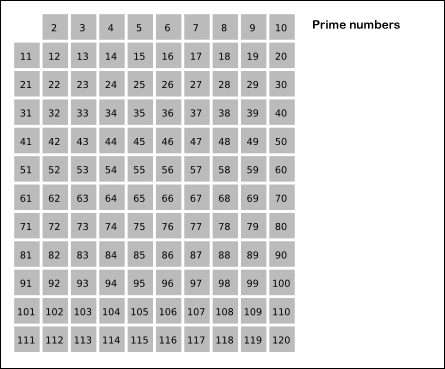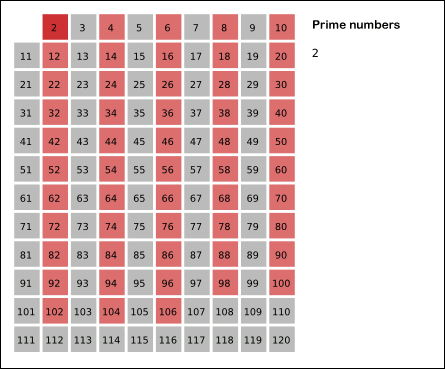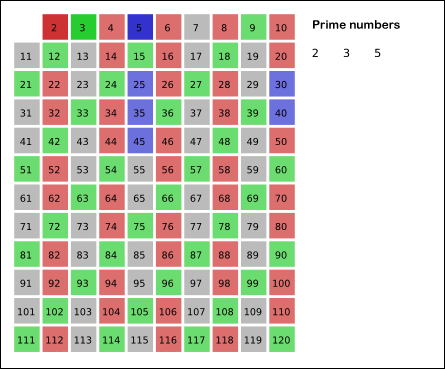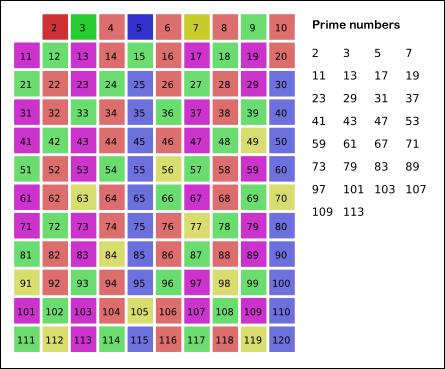
• 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
• 자기 자신을 제외한 7의 배수를 모두 지운다.
• 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
• 그림의 경우, $11^2 = 120$이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

출처: 위키백과

골드바흐의 추측

골드바흐의 추측(Goldbach’s conjecture)은 오래전부터 알려진 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 개의 소수(Prime number)의 합으로 표시할 수 있다는 것이다. 이때 하나의 소수를 두 번 사용하는 것은 허용한다.

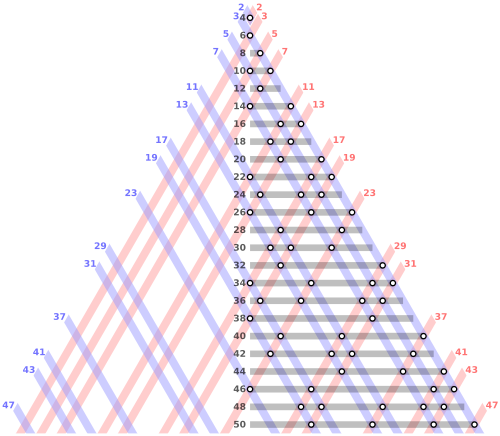
예를 들어, 50까지의 짝수는

4 = 2+2
6 = 3+3
8 = 3+5
10 = 3+7 = 5+5
12 = 5+7
14 = 3+11 = 7+7
16 = 3+13 = 5+11
18 = 5+13 = 7+11
20 = 3+17 = 7+13
22 = 3+19 = 5+17 = 11+11
24 = 5+19 = 7+17 = 11+13
26 = 3+23 = 7+19 = 13+13
28 = 5+23 = 11+17
30 = 7+23 = 11+19 = 13+17
32 = 3+29 = 13+19
34 = 3+31 = 5+29 = 11+23 = 17+17
36 = 5+31 = 7+29 = 13+23 = 17+19
38 = 7+31 = 19+19
40 = 3+37 = 11+29 = 17+23
42 = 5+37 = 11+31 = 13+29 = 19+23
44 = 3+41 = 7+37 = 13+31
46 = 3+43 = 5+41 = 17+29 = 23+23
48 = 5+43 = 7+41 = 11+37 = 17+31 = 19+29
50 = 3+47 = 7+43 = 13+37 = 19+31

위와 같이, 두 개의 소수의 합으로 표현할 수 있다. 그러나 모든 짝수에서 가능한지는 아직까지 해결하지 못하고 있다.

알고리즘 과정

에라토스테네스의 체의 관한 문제는 앞선 문제풀이들에서 많이 다뤘으니 깊이 설명하지 않고 넘어갈게요~ 대신 링크는 아래 남겨둘테니 참고하고 싶으시다면 보시는 것도 좋을 것 같아요 소수에 관련된 문제에서는 계속 등장하니까요!

백준 1929 소수구하기 백준 4948 베르트랑 공준

먼저 이 문제를 풀 때 머리속으로 알고리즘을 떠올린 과정을 설명드리자면 소수 구하는 것은 문제가 10000보다 작거나 같은 수를 기준으로 하기에 10000까지의 배열을 먼저 생성해주고 미리 에라토스테네스의 체를 사용하여 10000까지의 수의 소수 판별을 해놓는 게 먼저였습니다.

“다음으로 이 문제를 어찌하면 조금 더 효율적으로 풀 수 있을까?”라고 생각을 했습니다. 왜냐하면 노가다로는 누구든 에라토스테네스의 체를 이용하면 풀 수 있을 것 같았습니다.

이 문제에서 요구한 사항은 "두 소수의 차이가 최소인 것이 먼저 나와야한다.” 라고 했기에 여기서 착안한 방법으로 두 소수의 차이를 적게하려면 그 수를 반으로 나눈 것에 두 수가 가까우면 가능하겠다! 라고 생각했습니다.

경우를 나눠서 생각해봤습니다.

1. 수를 반으로 나눴는데 때마침 그 수가 `소수일 경우`
2. 수를 반으로 나눴지만 그 수가 소수가 `아닐 경우`

1번의 경우 바로 반반씩 출력해주면 끝이납니다.

1. 2번의 경우가 중요한데 반으로 나눈 수를 1씩 감소시킵니다.
2. 감소된 수를 소수인지 판별합니다.
3. 소수로 판별된다면 전체에서 남은 수도 소수인지 판별합니다.
4. 두 숫자 모두 소수라면 그대로 출력해주고 break를 걸어 중지시켜줍니다.

다행히도 아니면 어쩌지 했지만 바로 성공했습니다!가 떴고 지금 이렇게 블로그에 신나서 남기고 있네용 :)

나머지 구체적인 코드는 아래에서 확인해주시면 될 것 같습니다! ㅎㅅㅎ

---

코드