[Baekjoon] 3053 택시 기하학
[Bronze III] 택시 기하학 - 3053
성능 요약
메모리: 14516 KB, 시간: 124 ms
분류
기하학(geometry), 수학(math)
문제 설명
19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.
택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
D(T1,T2) = |x1-x2| + |y1-y2|
두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.
따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합
반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
택시 기하학
- 맨해튼 거리
미국 뉴욕의 맨해튼처럼 바둑판 격자 모양으로 도로가 나있는 상황에서, 한 지점에서 다른 위치로 이동하기 위해서 필요한 거리를 뜻한다. 도로가 바둑판 격자처럼 되어 있으니 도로를 따라 이동해야 하는데, 이때의 이동거리가 두 점 사이의 거리가 된다.
예를 들어 이차원 평면에서 두점 P(p1, p2)와 Q(q1, q2)에 대해서 두 점 사이의 거리는 아래와 같다.
D(T1,T2) = |x1-x2| + |y1-y2|
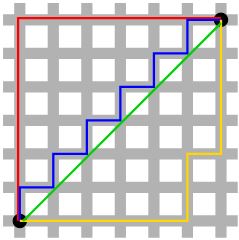
위의 그림이 이해하기 되게 쉬운 것 같다.
우리가 보통 아는 기하학이 문제에서 나오는 유클리드 기하학이다.
그런 유클리드 기하학으로 봤을 때 저 그림에서의 거리는 초록색이다.
하지만 택시 기하학으로 보았을 때 거리는 위에 공식으로 보면 알듯이 쉽게 말하면 가로의 길이 + 세로의 길이라고 생각하면 되고
정확히는 x좌표 차 + y좌표 차라고 생각하면 된다.
빨간색, 파란색, 초록색 선을 보면 구불구불하고 커브도 있는데 이러한 길이 다 현재 택시 기하학으로 보면 같은 거리에 속한다.
- 원
유클리드 기하학에서 원은 한점에서 같은 거리에 있는 점의 집합으로 표현된다. 그런데, 택시 기하학에서는 거리의 정의가 다르다 보니 원의 모습도 다르게 나타난다.
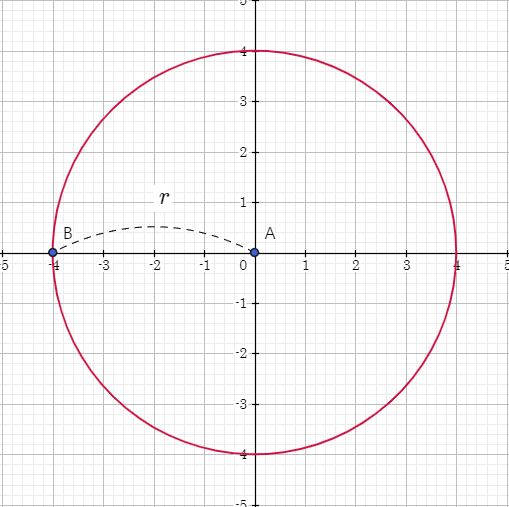
위에 그림은 보통 유클리드 기하학에서 볼 수 있는 원이다.
이 원의 넓이는 $𝜋r^2 = 𝜋 * r * r$ 로 구할 수 있다.
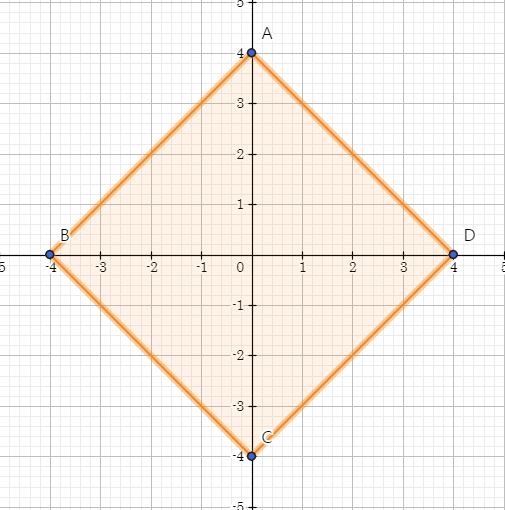
위의 그림은 이제 원을 택시 기하학으로 보았을 때의 원이라고 할 수 있다.
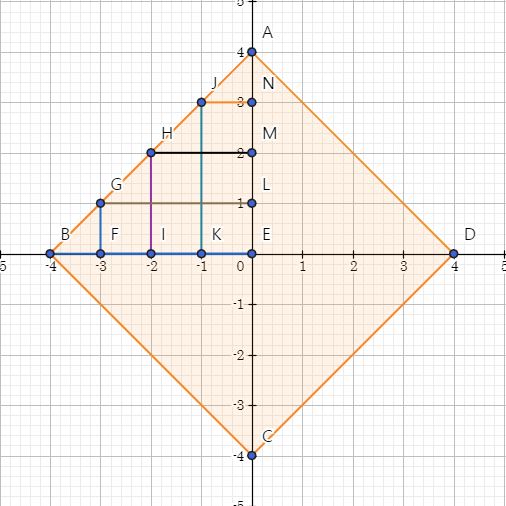
이렇게 보면 좀 이해가 되실 것 같은데 택시 기하학에서의 원은 한 점에서 택시 기하학적 거리가 같은 모든 점을 그려 연결하는 것이다. 다 거리가 4로 통일되어있다.
결국은 마름모 모양으로 정사각형을 45도 기울인 모양이 된다.
알고리즘 과정
이 문제는 브론즈 문제로 굉장히 쉽게 풀 수 있지만 나는 택시 기하학이라는 것을 잘 몰랐고 문제를 보고도 이해를 하지 못해서 이것저것 찾아보았다. 결국 이해하면 굉장히 쉽게 풀 수 있는 문제이다.
사실 블로그에는 최소 실버 이상의 문제만 올리려고 했었는데…생각보다 모든 문제들이 어떤 점에서는 공부할 점이 있다는 것을 깨닫고 올리게 되었다. 앞으로도 종종 브론즈 문제를 풀다가 잘 모르거나 공부할 점이 있는 문제들을 올리도록 할 것이다.
알고리즘이랄 것도 없이 위에 설명한 내용을 이해한다면 유클리드 기하학에서의 원의 넓이는 $𝜋r^2$이고 택시 기하학에서의 원의 넓이는 $2r^2$이 된다.
코드

Leave a comment