[Baekjoon] 2477 참외밭

[Silver IV] 참외밭 - 2477

문제 링크

성능 요약

메모리: 12864 KB, 시간: 108 ms

분류

애드 혹(ad_hoc), 기하학(geometry), 구현(implementation)

문제 설명

시골에 있는 태양이의 삼촌 댁에는 커다란 참외밭이 있다. 문득 태양이는 이 밭에서 자라는 참외가 도대체 몇 개나 되는지 궁금해졌다. 어떻게 알아낼 수 있는지 골똘히 생각하다가 드디어 좋은 아이디어가 떠올랐다. 유레카! 1m²의 넓이에 자라는 참외 개수를 헤아린 다음, 참외밭의 넓이를 구하면 비례식을 이용하여 참외의 총개수를 구할 수 있다.

1m²의 넓이에 자라는 참외의 개수는 헤아렸고, 이제 참외밭의 넓이만 구하면 된다. 참외밭은 ㄱ-자 모양이거나 ㄱ-자를 90도, 180도, 270도 회전한 모양(┏, ┗, ┛ 모양)의 육각형이다. 다행히도 밭의 경계(육각형의 변)는 모두 동서 방향이거나 남북 방향이었다. 밭의 한 모퉁이에서 출발하여 밭의 둘레를 돌면서 밭경계 길이를 모두 측정하였다.

예를 들어 참외밭이 위 그림과 같은 모양이라고 하자. 그림에서 오른쪽은 동쪽, 왼쪽은 서쪽, 아래쪽은 남쪽, 위쪽은 북쪽이다. 이 그림의 왼쪽위 꼭짓점에서 출발하여, 반시계방향으로 남쪽으로 30m, 동쪽으로 60m, 남쪽으로 20m, 동쪽으로 100m, 북쪽으로 50m, 서쪽으로 160m 이동하면 다시 출발점으로 되돌아가게 된다.

위 그림의 참외밭 면적은 6800m²이다. 만약 1m²의 넓이에 자라는 참외의 개수가 7이라면, 이 밭에서 자라는 참외의 개수는 47600으로 계산된다.

1m²의 넓이에 자라는 참외의 개수와, 참외밭을 이루는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이가 순서대로 주어진다. 이 참외밭에서 자라는 참외의 수를 구하는 프로그램을 작성하시오.

입력

첫 번째 줄에 1m²의 넓이에 자라는 참외의 개수를 나타내는 양의 정수 K (1 ≤ K ≤ 20)가 주어진다. 참외밭을 나타내는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이 (1 이상 500 이하의 정수) 가 둘째 줄부터 일곱 번째 줄까지 한 줄에 하나씩 순서대로 주어진다. 변의 방향에서 동쪽은 1, 서쪽은 2, 남쪽은 3, 북쪽은 4로 나타낸다.

출력

첫째 줄에 입력으로 주어진 밭에서 자라는 참외의 수를 출력한다.

---

알고리즘 과정

처음에 이 문제를 풀 때는 어쩌피 길이의 한계도 주어져 있었고 배열로 직사각형을 구현하여 풀려고 하였다.

문제점이 많았는데 고쳐보려고 했지만 실패했다.

문제는 일단 직사각형의 출발점이 정해져 있지 않은 임의의 한 점이였고, 반시계 방향이라 하다보니 배열 좌표로 입력하려다 보니 음수로 가는 경우도 생기고 여러가지로 문제가 많았다.

그래서 결국 찾아봤지만…이거 원래 이렇게 풀도록 문제가 설계된 게 맞는지 살짝 의문스럽다.

사실 지금 푸는 이 방법은 방향을 입력하는 것도 의미가 없어지고 음…뭐야 이게 싶은 느낌? 나만 그런가?

간단하게 설명하자면 기하학적으로 푸는 문제였던 것? 같다.

입력받은 변들을 모두 곱하여 겹치는 부분중에 덜겹치는 부분이 빼야하는 값으로 나오는 것 같다.

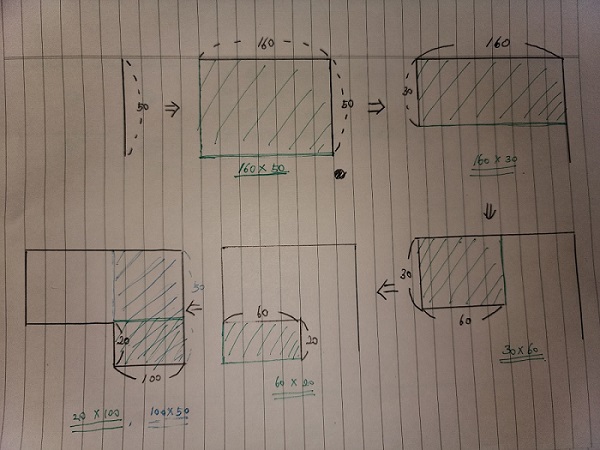
각 변 입력할 때마다 곱하고 마지막 첫변과 마지막 변까지 곱해준다면 아래 사진처럼 각 부분이 3번씩 나오는 겹치는데 빠지는 부분은 2번씩 겹친다.

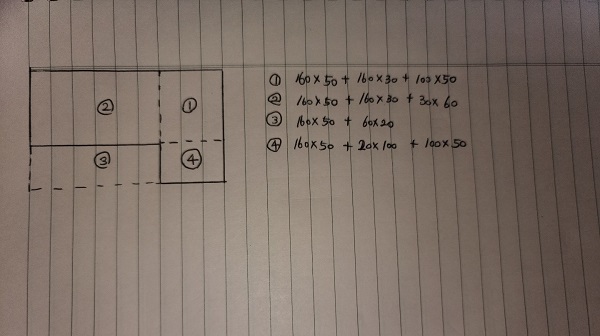
사진에 나와있는 건 1, 2, 3, 4 구역이 어디의 변을 곱했을 때 나왔는지를 나타내보았다.

이처럼 결국

(각 변의 곱 중 제일 큰 값 X 3) - (각 변의 곱의 합) = 직사각형의 빠진 부분의 넓이

해주면 풀 수 있다.

---

코드