[Baekjoon] 1929 소수 구하기

[Silver III] 소수 구하기 - 1929

문제 링크

성능 요약

메모리: 37832 KB, 시간: 1280 ms

분류

수학(math), 정수론(number_theory), 소수 판정(primality_test), 에라토스테네스의 체(sieve)

문제 설명

M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 자연수 M과 N이 빈 칸을 사이에 두고 주어진다. (1 ≤ M ≤ N ≤ 1,000,000) M이상 N이하의 소수가 하나 이상 있는 입력만 주어진다.

출력

한 줄에 하나씩, 증가하는 순서대로 소수를 출력한다.

---

에라토스테네스의 체(sieve)

수학에서 에라토스테네스의 체는 소수를 찾는 방법이다. 고대 그리스 수학자 에라토스테네스가 발견하였다.

• 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
• 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
• 자기 자신을 제외한 2의 배수를 모두 지운다.
• 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
• 자기 자신을 제외한 3의 배수를 모두 지운다.
• 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
• 자기 자신을 제외한 5의 배수를 모두 지운다.
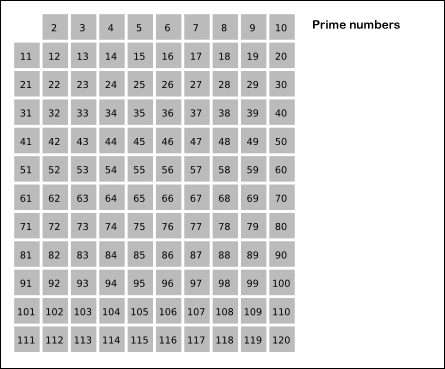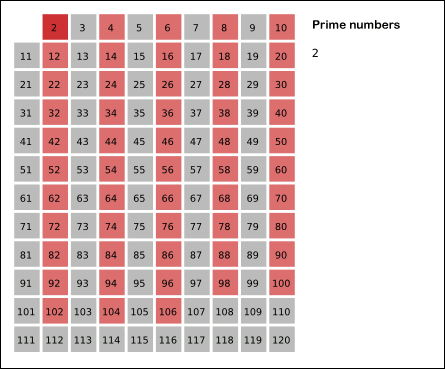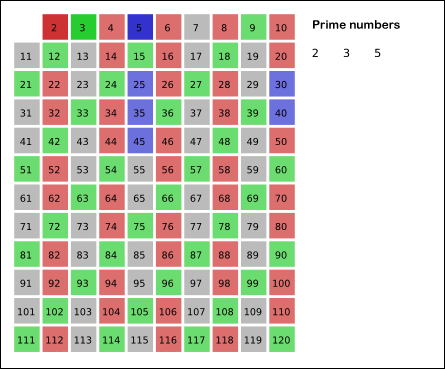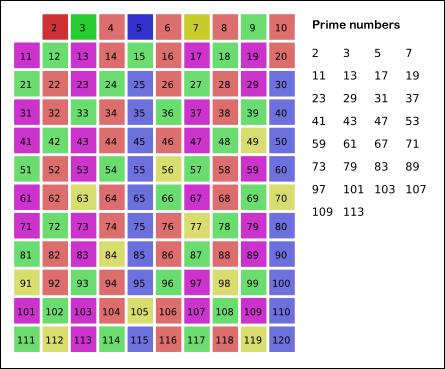
• 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
• 자기 자신을 제외한 7의 배수를 모두 지운다.
• 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
• 그림의 경우, $11^2 = 120$이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

출처: 위키백과

알고리즘 과정

먼저 위에 에라토스테네스의 체라는 소수를 찾는 방법은 소수관련 알고리즘을 풀어봤다면 알 법한 방법이다.

다시 말하자면, 그만큼 많이 쓰이는 알고리즘인 것 같다.

현재 이 문제를 풀 때는 정말 시간이 얼마 걸리지 않았는데 그 이유는 baekjoon Algorithm 2581 소수 문제를 풀면서 정말 똑같은 풀이로 풀었었기 때문이다.(물론 그 때 다른 방식으로 풀었는데 틀리다고 해서 찾아봤음..)

알고리즘을 내가 이해한대로 풀어보자면 일단 숫자의 배열을 만들어 소수와 소수가 아닌 수를 판별하기 위해 boolean prime[]배열을 만든다.

prime[]배열은 소수이면 false로 표시되고 소수가 아니면 true로 표시된다.

0과 1은 당연히 소수에서 제외되니까 먼저 true로 표시한다.

이제 소수인 2, 3, 5, 7 등 소수들을 정하기엔 어려우니 for문을 통해 2부터 배수를 해줄 수의 범위를 만들어준다.

for(int i = 2; i*i <=N; i++)

그 for()문 안에 위에 for문에서 처럼 범위를 잡으면 2의 배수와 4의 배수같이 겹치는 것이 많이 있을테니 if문을 통해 false인 것만 골라서 prime[] = false 해주고 for()문을 통해 배수들을 전부 차례대로 제거해준다.

if (!prime[i]) { // false가 소수
  for (int j = i*i; j <= N; j += i) {
    prime[j] = true;
  }
}

바보같이 “나는 여기서 아니 이렇게하면 N = 15일 경우에 3의 배수로 지워지는거지 5의 배수들은 25 <= 15로 인해서 5의 배수들중에 생략되는 게 있을 거 아냐!” 라는 생각을 잠시 했지만 여러분은 그런 실수를 안하리라 믿는다… 나는 바보

결국 어쩌피 겹치지 않는 배수의 시작은 그 숫자의 제곱부터 시작이다. 5의 배수중 안겹치는건 25부터라고 생각하면 쉽다. 사실 나만 쉬운거지 딴 사람한텐 당연했겠지..?

나머지는 이제 범위에 든 수 중에 소수로 남은 수를 출력해주면 끝이 난다.

---

코드