[Baekjoon] 1002 터렛
[Silver IV] 터렛 - 1002
성능 요약
메모리: 14384 KB, 시간: 160 ms
분류
기하학(geometry), 수학(math)
문제 설명
조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다. 다음은 조규현과 백승환의 사진이다.
이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.
조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.
출력
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
알고리즘 과정
이 문제는 친절하게 대놓고 변수 이름부터 원을 이용하라고 알려주는 것 같습니다 ㅎㅅㅎ…
저는 보통 뭔가 풀 방법이 생각나거나 했을 때 바로 코드로 적기보다는 메모장에 어찌할지 써놓고 하는 편이에요(정말 대강!)
왜냐하면 머리가 나빠서 잘 까먹더라고요 “내가…뭘…하려고…했드라?” 이런 느낌
이 문제가 마린의 좌표를 구하는 문제는 아니기에 두 원의 위치관계의 따른 접점의 개수로 판단하면 되겠다고 생각했습니다.
경우를 접점의 개수로 나눠보면 0, 1, 2, 무한으로 나눠볼 수 있을 것 같습니다.
물론 거리를 구하는 공식은 다들 학창시절 때 해보셨겠지만 아래 공식을 이용하면 됩니다.
거리^2 = (x좌표의 차)^2 + (y좌표 차)^2
이 글에선 제곱을 Math.pow()를 이용하여 풀 것 입니다.
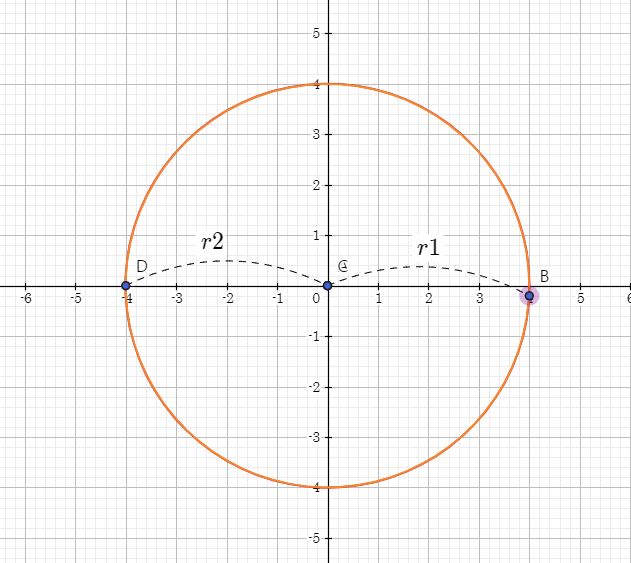
- 접점의 개수가 무한일 경우
그림을 그려봤는데 잘 분간이 안가실 것 같긴하네요
그림은 현재 두 원이 같은 터렛의 위치, 같은 거리의 마린의 위치를 가지고 있습니다.
이렇게 되면 마린이 원의 테두리 안에서 무한히 존재할 수 있는 경우의 수를 가지고 있습니다.
식은 터렛간의 좌표가 같고 마린까지의 거리가 같다고 하면 됩니다.
if(x1 == x2, y1 == y2, r1 == r2)
- 접점의 개수가 0개일 경우
접점의 개수가 0개인 경우는 솔직히 좀 헷갈리는 면이 있습니다.
이 경우들은 이 문제에서 성립이 되지 않는 상황이여서 그것에 관해 갑자기 머리속이 복잡해졌는데 아마 제가 지금 코로나에 걸렸는데 약을 한 번에 9개씩 때려붓고 헤롱헤롱해서 그럴수도 있어요…
글씨가 눈에 안들어와요..코로나 조심하세요 여러분 애들이 약하대서 겁 안먹었는데 호되게 당하고 있습니다.
0개인 경우는 성립할 수 없다고 한 이유는 사실 이 문제가 터렛의 위치가 달라지는 것이지 사실 마린의 위치는 두 터렛에서 같은 마린을 측정하는 것입니다.
r1, r2는 사실 마린의 위치라고 봐도 무방합니다. 그런데 접점이 없다면 마린이 2마리 이상이 되야하기 때문에 성립할 수 없습니다.
입력을 애초에 성립이 되지 않는 경우를 하면 안되는 것 아닌지 아니면 조건을 붙여서 이런 케이스를 빼줘야하는 거 아닌지 이걸 0으로 하면 안되는거 아냐?! 하면서 혼자 헷갈리고 있었는데 그냥 경우의 수를 나타내주는 것이니 0으로 하면 되는 것 같습니다.
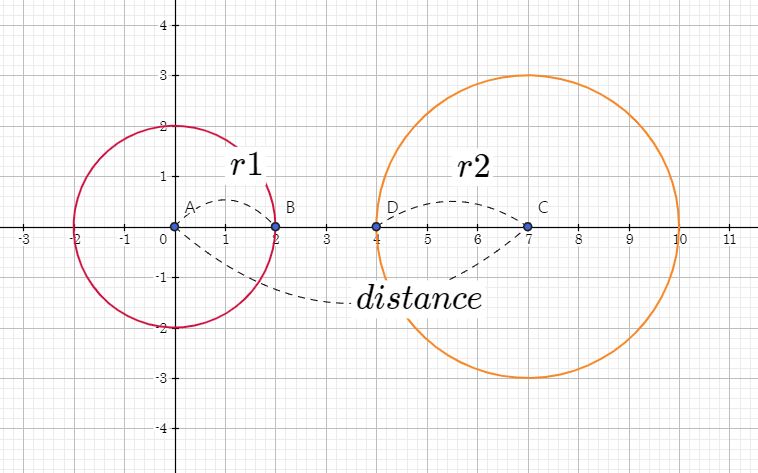
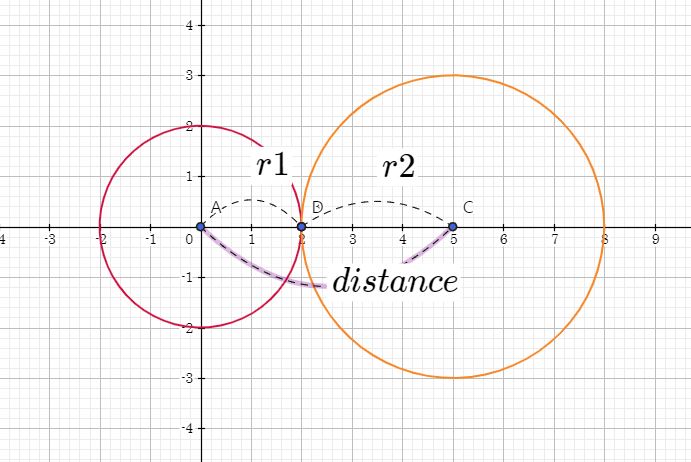
- 외부에서 접하지 않는 원
현재 그림은 터렛의 위치도 다르고 두 원의 원점도 다르고 두 원이 닿지 않고 있는 경우입니다.
이런 경우에는 원이 닿지 않고 있기도 하고 애초에 이 경우는 성립할 수 없는 게 다른 위치에서 같은 마린의 위치를 파악하는 것이라 외부에서 접하지 않은 원이라고 볼 수 있습니다.
식으로 표현하자면 터렛 사이간의 거리가 > 원의 반지름의 합한 길이라고 할 수 있습니다.
if(distance == Math.pow(r1 + r2, 2))
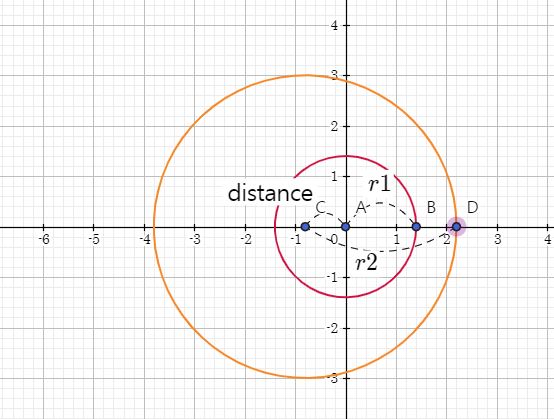
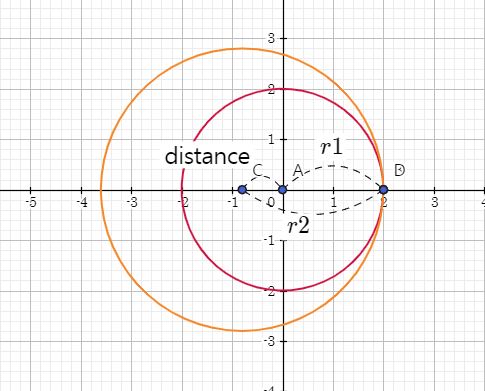
- 내부에서 접하지 않는 원
이 그림은 큰 원 내부에 작은 원이 들어가 있는 경우입니다.
위에 말한 것처럼 이 경우도 접점의 개수가 없는 경우이고, 결국 성립할 수 없으므로 0개로 파악됩니다.
식은 그림에서 보이다 싶이 반지름의 차를 터렛간의 거리로 비교해주면 됩니다.
if(distance < Math.pow(r1 - r2, 2))
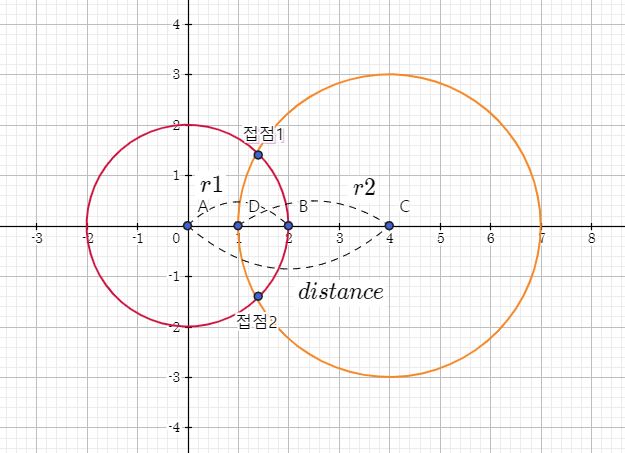
- 접점의 개수가 1개일 경우
접점의 개수가 1개인 경우는 외접하는 경우, 내접하는 경우 총 두 가지가 나옵니다.
- 외접하는 경우
외접하는 경우는 식으로 반지름의 합 = 터렛간의 거리 같습니다.
if(distance == Math.pow(r1 + r2, 2))
- 내접하는 경우
내접하는 경우는 외접과 비슷하지만 반지름의 차로 터렛간의 거리와 같다고 해주면 됩니다.
if(distance == Math.pow(r1 - r2, 2))
- 접점의 개수가 2개일 경우
마지막으로 접점의 개수가 2개일 경우인데 이 경우는 쉽게 처리할 수 있는 것이 앞에서 모든 경우의 수를 다 넣어놓았기 때문에 else로 처리하여 작성해주시면 됩니다.
이렇게 풀고 제가 제출을 했는데 분명히 틀린 것이 없어보였는데 무엇이 문제일까? 라고 계속 보다가 if문의 순서도 영향을 줄 수 있다는 것을 알게되었습니다.
왜냐하면 원안에 원이 있는 경우랑 원 두개가 같은 위치, 같은 반지름을 가지고 있는 경우를 나눠놓았는데 if문 처음에 같은 반지름과 같은 위치를 가지고 있는 식을 포함시키지 않으면 원 안에 원이 있는 경우도 해당될 수 있기 때문에 제대로 파악이 되지 않습니다!
따라서
if(x1 == x2, y1 == y2, r1 == r2)
위의 식은 아래식보다 먼저 나와야합니다.
if(distance < Math.pow(r1 - r2, 2))
코드

Leave a comment